Course / training:

Method for Logical Analysis

Combinatorische explosie in Logische systemen



Syntactische expansie.




6.

 

Syntactische variatie bij asymmetrische (binaire) connectieven.



(6.1)

Structuurvariatie bij asymmetrische ( binaire) connectieven.


Geneste structuren met asymmetrisch hoofdconnectief (binary trees).
Deze verzameling bevat het maximale aantal unieke 'minimale' varianten van geneste structuren met alleen precies -tweeplaatsige clusters: zgn. 'volle' binaire of dichotome (zoek)bomen (binary trees).
Ook hierin komen geen enkelvoudige nesten c.q. negaties voor en is onderscheid of volgorde van basiselementen en connectieven vooralsnog irrelevant.

tb*

(n1): de verzameling van alle unieke 'minimale' varianten van binaire geneste structuren voor n1 basiselementen.

Voorbeeld.


Bijv. Stel n1

=

3;

tb*

(n1)

:=

{ '(x(xx))', '((xx)x)' }.
Maximaal aantal is 2.
Bijv. Stel n1

=

4;

tb*

(n1)

:=

{ '((xx)(xx))', '(x(x(xx)))', '(x((xx)x))', '((x(xx))x)', '(((xx)x)x)', }.
Maximaal aantal is 5.
{ n1 (

tb *

(n1)

tm*

(n1) )n1 }.
NB. De verzamelingen

tc*

(n1) en

tb *

(n1) sluiten elkaar vrijwel altijd uit - afgezien van enkele eerste elementen.

Omvang.


tb(n1): het totale aantal elementen in verzameling

tb *

(n1).
De waarden tb(n1) zijn simpel afleidbaar met de functie voor zgn. Catalan getallen (of 'Schröder's first problem', ook genoemd Segner numbers).
Dit is reeks A000108 (eerder M1459, N0577) in de OEIS.
De expliciete formule luidt:
{ tb(0)

=

0;
n1 ( (n1

>

0 ) ( tb(n1)

:=

Catalan

(n1 -1 );

:=

((2 ·(n1 -1 ) )

!

/ (n1 ·(n1 -1 )

!

) );

:=

A000108(n1 -1 )

|

(offset 0 ) ) )n1 }.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16);
tb(n1)

=

{ 0, 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,
16796, 58786, 208012, 742900, 2674440, 9694845 }.

(6.2)

Valentievariatie bij asymmetrische (binaire) connectieven.


Voor valentievariatie in binair geneste structuren gelden mutatis mutandis dezelfde kanttekeningen als die in het geval van (algemene) symmetrische boomstructuren (zie 4.2).

(6.2.1)

Valentievariatie bij basiselementen.


(6.2.1a)

Totaal aantal (occurrences) van leaves:


Omvang.


Ab(n1): het totale aantal eindelementen in alle mogelijke 'minimale' binaire geneste structuren met elk n1 eindelementen.
Berekening analoog aan die van Am(n1) resp. Ac(n1).
De waarden Ab(n1) komen goeddeels overeen met reeks A000984, type B Catalan numbers, Central binomial coefficients, in de OEIS.
{ Ab(0)

=

0; n1 ( (n1

>

0 ) ( Ab(n1)

:=

A000984(n1 -1 )

|

(offset 0 ) ) ) )n1 }.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16);
Ab(n1)

=

{ 0, 1, 2, 6, 20, 70, 252, 924, 3432, 12870, 48620,
184756, 705432, 2704156, 10400600, 40116600, 155117520 }.
(6.2.1b)

Valentievariatie over leaves:


tbv*A

(n1): de verzameling

tb*

(n1) uitgebreid met alle unieke valentievariaties over eindelementen.

Voorbeeld.


Bijv. Stel n1

=

2;

tbv *A

(n1):

:=

{ '(x,x)', '(x,¬x)', '(¬x,x)', '(¬x,¬x)' }.
Maximaal aantal is 4.
Bijv. Stel n1

=

3;

tbv *A

(n1):

:=

{ '(x(xx)))', '((xx)x))', '(x(x¬x)))', '((xx)¬x))', '(x(¬x¬x)))', '((x¬x)¬x))', '(x(¬xx)))', '((x¬x)x))', '(¬x(xx)))', '((¬xx)x))', '(¬x(x¬x)))', '((¬xx)¬x))', '(¬x(¬xx)))', '((¬x¬x)x))', '(¬x(¬x¬x)))', '((¬x¬x)¬x))' }.
Maximaal aantal is 16.
{ n1 (

tb *A

(n1)

tb v*A

(n1) )n1 }.

Omvang.


tbv*A(n1): het totale aantal elementen in verzameling

tbv*A

(n1).
Berekening analoog aan die van tmvA(n1) resp. tc vA(n1).
De waarden tbvA(n1) komen goeddeels overeen met reeks A025225 resp. A115125 in de OEIS.
{ tbvA(0)

=

0; t bvA(1)

=

1; v

|

n1 ( (n1

>

1 ) ( tbvA(n1)

:=

A025225(n1 -1 )

|

(offset 1 ) ) ) )n1, v }.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16);
tbvA(n1)

=

{ 0, 2, 4, 16, 80, 448, 2688, 16896, 109824, 732160, 4978688,
34398208, 240787456, 1704034304, 12171673600, 87636049920, 635361361920 }.

(6.2.2)

Valentievariatie bij nesten.


(6.2.2a)

Totaal aantal (occurrences) van nests:


Omvang.


Nb(n1): het totale aantal nesten in alle mogelijke 'minimale' binaire geneste structuren met elk n1 eindelementen.
Omdat in

tb*

(n1) het aantal nesten per boom constant is, wijkt de berekening van Nb(n1) af van die van Nm(n1) en Nc(n1).
De waarden Nb(n1) komen goeddeels overeen met reeks A001791 in de OEIS.
{ Nb(0)

=

0; Nb(1)

=

1;
n1 ( (n1

>

1 ) ( Nb(n1)

:=

binomial

((2

*

(n1 -1 ) ), (n1 -2 ) );

:=

(n1 -1 )

*

Catalan

(n1 -1 );

:=

(n1 -1 )

*

tb(n1);

:=

A001791(n1 -1 )

|

(offset 1 ) ) )n1 }.
Bijv. Stel n1

=

3; Nb(n1)

:=

(

binomial

((2

*

(3 -1 ) ), (3 -2 ) )

=

((3 -1 )

*

(tb(3)

=

2 )

=

) 4.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16);
Nb(n1)

=

{ 0, 1, 1, 4, 15, 56, 210, 792, 3003, 11440, 43758,
167960, 646646, 2496144, 9657700, 37442160, 145422675 }.
(6.2.2b)

Valentievariatie over nests:


tbv*N

(n1): de verzameling

tb*

(n1) uitgebreid met alle unieke valentievariaties over nesten .
{ v

|

n1 (

t b*

(n1)

tb v*N

(n1) )n1, v }.

Omvang.


tbvN(n1): het totale aantal elementen in verzameling

tbv*N

(n1).
De waarden tbvN(n1) komen goeddeels overeen met reeks A052701 in de OEIS.
{ tbvN(0)

=

0; tbvN(1)

=

2;
v

|

n1 ( (n1

>

1 ) ( tbvN(n1)

:=

Catalan

(n1 -1 )

*

v**(n1 -1 );

:=

tbvA(n1) /2;

:=

A052701(n1 -1 ) ) )n1, v }.
Bijv. Stel n1

=

3; tbv N(n1)

:=

(tbvA(n1) /2

=

) 8.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16);
tbvN(n1)

=

{ 0, 2, 2, 8, 40, 224, 1344, 8448, 54912, 366080, 2489344,
17199104, 120393728, 852017152, 6085836800, 43818024960, 317680680960 }.

(6.2.3)

Valentievariatie over basiselementen èn nesten.


(6.2.3a)

Totaal aantal (occurrences) van nodes (leaves èn nesten):


Omvang.


Kb(n1): het totale aantal nodes (leaves èn nesten) in alle mogelijke 'minimale' binaire geneste structuren met elk n1 eindelementen.
Berekening analoog aan die van Km(n1) (en niet van Kc(n1 )!).
De waarden Kb(n1) komen goeddeels overeen met reeks A001700 in de OEIS.
Kb(0)

=

0; Kb(1)

=

2; n1 ( (n1 > 1 ) ( Kb(n1)

:=

A001700(n1 -1 )

|

(offset 0 ) ) )n1 }.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16);
Kb(n1)

=

{ 0, 2, 3, 10, 35, 126, 462, 1716, 6435, 24310, 92378,
352716, 1352078, 5200300, 20058300, 77558760, 300540195 }.
(6.2.3b)

Valentievariatie over nodes (leaves èn nesten):


tbv*K

(n1): de verzameling

tb*

(n1) uitgebreid met alle unieke valentievariaties over eindelementen en nesten.
{ v

|

n1 (

t bv*K

(n1)

:=

t bv*A

(n1)

tbv*N

(n1) )n1, v }.

Omvang.


tbvK(n1): het totale aantal elementen in verzameling

tbv*K

(n1).
Berekening is analoog aan die van tmvK(n1) (en niet van t cvK(n1)!).
De waarden tbvK(n1) komen goeddeels overeen met reeks A052707 in de OEIS.
{ tbvK(0)

=

0; t bvK(1)

=

4; v

|

n1 ( (n1

>

1 ) ( tbvK(n1)

=

A052707(n1 -1 )

|

(offset 0 ) ) )n1, v }.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16);
tbvK(n1)

=

{ 0, 4, 8, 64, 640, 7168, 86016, 1081344, 14057472, 187432960, 2549088256,
35223764992, 493132709888, 6979724509184, 99710350131200, 1435829041889280, 20819521107394560 }.

(6.3)

Volgordevariatie bij asymmetrische (binaire) connectieven.


Kiezen we voor asymmetrische connectieven, zoals (unidirectionele) implicaties, dan moeten we uiteraard zeker rekening houden met alle verschillende volgordes van basiselementen binnen de redeneervormen.
(6.3.1)

Volgordevariatie bij basiselementen.


(6.3.1a)

Geldige permutaties (faculteiten) voor volgordes van leaves:


Gelijk aan de waarden F(n1) als vermeld voor de algemene meerplaatsige boomstructuren.
(6.3.1b)

Volgordevariatie over leaves:


tbv,o*A

(n1): de verzameling

tbv*A

(n1) uitgebreid met alle unieke volgordevariaties over eindelementen.
{ v

|

n1 (

t bv*A

(n1)

tbv,o*A

(n1) )n1, v }.

Voorbeeld.


Analoog aan die van

tmv,o*A

(n1).

Omvang.


tbv,o*A(n1): het totale aantal elementen in verzameling

tbv,o*A

(n1).
Berekening analoog aan die van tmv,o*A(n1).
De waarden tbv,oA(n1) komen goeddeels overeen met reeks A052713 in de OEIS.
{ n1 ( (n1 ≥ 0 ) ( tbv,oA(n1)

:=

A052713(n1 )

|

(offset 0 ) ) )n1 }.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16);
tbv,oA(n1)

=

{ 0, 2, 8, 96, 1920, 53760, 1935360, 85155840, 4428103680, 265686220800, 18066663014400,
1373066389094400, 115337576683929600, 10611057054921523000, 1.0611057054921523e+21, 1.1459941619315245e+23, 1.3293532278405684e+25 }.
NB. De verzamelingen

tcv,o*A

(n1) en

t bv,o*A

(n1) sluiten elkaar vrijwel altijd uit - afgezien van enkele eerste elementen.

(6.3.2)

Volgordevariatie bij nesten.


Zoals gezegd telt volgordevariatie niet voor nesten.

(6.3.3)

Volgordevariatie over nodes (leaves èn nesten):


tbv,o*K

(n1): de verzameling

tbv*K

(n1) uitgebreid met alle unieke volgordevariaties over (alleen) eindelementen.
{ v

|

n1 (

t bv*K

(n1)

tbv,o*K

(n1) )n1, v }.

Omvang.


tbv,o*K(n1): het totale aantal elementen in verzameling

tbv,o*K

(n1).
De volgordevariaties over eindelementen gelden voor de gehele gecombineerde i.e. produktverzameling tb vK(n1).
Berekening is analoog aan die van tmv,o*K(n1) (maar niet die van tcv,o*K(n1) ).
De waarden tbv,oK(n1) komen goeddeels overeen met reeks A052737 in de OEIS.
{ tbvA(0)

=

0; t bvA(1)

=

2; n1 ( (n1

>

1 ) ( tbvA (n1)

:=

A052737(n1 )

|

(offset 0 ) ) )n1 }.
Bijv. Stel n1

=

3; tbv,o* K(n1)

:=

((tbvK(n1 )

=

64 )

*

(P(n1)

=

6 )

=

) 384.
Bijv. Voor n1

=

0,1,2,3,

..

(t·(v,d)

=

16);
tmv,oK(n1)

=

{ 0, 4, 16, 384, 15360, 860160, 61931520, 5449973760, 566797271040, 68015672524800, 9250131463372800,
1406019982432665600, 236211357048687820000, 4.346288969695856e+22, 8.692577939391712e+24, 1.8775968349086097e+27, 4.3560246569879746e+29 }.

(6.4)

Connectiefvariatie bij asymmetrische (binaire) connectieven.


In binaire boomstructuren hebben we enkel te maken met de verzameling asymmetrische c.q. unidirectionele connectieven: implicatie en inverse implicatie).
{ (

Cb*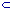

=

{ ' ', '' } );
c1

:=

|

Cb *

|

;

:=

2 }.

(6.4.1)

Connectiefvariatie bij basiselementen.


Zoals gezegd niet van toepassing.

(6.4.2)

Connectiefvariatie bij nesten.


(6.4.2a)

Connectiefvariatie per nest opgeteld:


Omvang.


Cb(n1,c1): de connectiefvariatie van alle nesten in de elementen in een verzameling

tb*

(n1) opgeteld bij c1 connectiefsymbolen.
Voor de connectiefvariatie in binaire geneste structuren gelden dezelfde kenmerken als van die in (algemene) meerplaatsige geneste structuren in normaalvorm (d.i. tot diepteniveau twee). Omdat het aantal connectiefsymbolen c1 hier eveneens beperkt is tot 2, is ze onafhankelijk van het aantal nesten en is de berekening analoog aan die van Cc(n1,c1).
De waarden Cc(n1,c1) komen goeddeels overeen met reeks A068875 in de OEIS.
{ Cb(n1,c1)

=

0; n1 ( (n1

>

0 ) ( Cb(n1,c1)

:=

A068875(n1 -1 )

|

(offset 0 ) ) )n1 }.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16); c1

=

2;
Cb(n1,c1)

=

{ 0, 1, 2, 4, 10, 28, 84, 264, 858, 2860, 9724,
33592, 117572, 416024, 1485800, 5348880, 19389690 }.
(6.4.2b)

Connectiefvariatie over nests:


tbv,[o,]c*N

(n1,c1): de verzameling

tb*N

(n1): uitgebreid met alle unieke connectiefvariaties over nesten bij c1 connectiefsymbolen.
(n1 c1 (

tbv*N

(n1)

tbv,[o,]c*N

(n1,c1) )c1, n1 ).

Omvang.


tbv,[o,]c*N(n1,c1): het totale aantal elementen in verzameling

tbv,[o,]c*N

(n1,c1).
Hierin telt wel de valentievariantie over nesten mee.
De waarden tbv,oA(n1) komen goeddeels overeen met reeks A025225 in de OEIS.
{ v

|

n1 ( (t b(n1)

:=

|

tb*

(n1)

|

);
m1 ( (m1

:=

t b(n1) );
c1 ( (c1

<

3 );
( tbv,[o,]cN(n1,c1)

:=

tbv[,o]N(n1) *c1;

:=

tbvA(n1) ) )c1 )m1 )n1, v }.
( tbv,[o,]cN(n1,c1)

=

0; n1 ( (n1

>

0 ) tbv,[o,]cN(n1,c1)

:=

A025225(n1 -1 )

|

(offset 1 ) ) )n1 ) }.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16); c1

=

2;
tbv,[o,]cN(n1,c1)

=

{ 0, 2, 4, 16, 80, 448, 2688, 16896, 109824, 732160, 4978688,
34398208, 240787456, 1704034304, 12171673600, 87636049920, 635361361920 }.

(6.4.3)

Connectiefvariatie over nodes (leaves èn nesten):


(6.4.3a)

Connectiefvariatie per node opgeteld:


Omvang.


Deze is uiteraard gelijk aan die bij nesten.
(6.4.3b)

Connectiefvariatie over nodes (leaves èn nesten):


tbv,o,c*K

(n1,c1): de verzameling

tbv,o*K

(n1) uitgebreid met alle unieke connectiefvariaties over (alleen) nesten bij c1 connectiefsymbolen.
{ n1 c1 (

tbv,o*K

(n1)

tbv,o,c*K

(n1,c1) )c1, n1 }.

Omvang.


tbv,o,c*K(n1,c1): het totale aantal elementen in verzameling

tbv,o,c*K

(n1,c1).
Berekening is in principe analoog aan die van tmv,o,c*K( n1,c1), zij het wat betreft de connectiefvariatie analoog aan die van tcv,o,c *K(n1,c1).
NB. De waarden tbv,o,cK(n1,c1) komen niet voor als reeks in de OEIS.
{ v

|

n1 ( (t b(n1)

:=

|

tb*

(n1)

|

);
m1 ( (m1

:=

t b(n1) );
c1 ( (c1

<

3 );
( tbv,o,cK(n1,c1)

:=

tbv,oK(n1) *c1 ) )c1 )m1 )n1, v }.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16); c1

=

2;
tbv,o,cK(n1,c1)

=

{ 0, 4, 32, 768, 30720, 1720320, 123863040, 10899947520, 1133594542080, 136031345049600, 18500262926745600,
2812039964865331000, 472422714097375640000, 8.692577939391712e+22, 1.7385155878783424e+25, 3.7551936698172195e+27, 8.712049313975949e+29 }.
NB. Deze reeks is nog niet hyperexponentieel.

(6.5)

Deelverzamelingen per lengte bij asymmetrische (binaire) connectieven.



(6.5.1)

Binomiaal coëfficiënten:


Gelijk aan de waarden B(t·(v,d), n1) als vermeld voor de algemene meerplaatsige boomstructuren.

(6.5.2)

Subsets (per lengte) over nodes (leaves èn nesten):


tbv,o,c,s*K

(n1,c1): de verzameling met alle unieke verzamelingen

tbv,o,c*K

(n1,c1) van 'minimale' syntactische varianten over eindelementen en nesten binnen maximaal-tweeplaatsige geneste structuren met elk n1 unieke basiselementen, inclusief valentievarianten, volgordevarianten en connectiefvarianten bij c1 connectiefsymbolen.
{ n1 c1 (

tbv,o,c,s*K

(n1,c1)

tbv,o,c*K

(n1,c1) )c1, n1 }.

Omvang.


tbv,o,c,sK(n1,c1): het totale aantal elementen in verzameling

tbv,o,c,s*K

(n1,c1).
Berekening analoog aan die van tmv,o,c,sK(n1,c1) en van tcv,o,c,sK(n1,c1).
NB. De waarden tbv,o,c,sK(n1,c1) komen niet voor als reeks in de OEIS.
Bijv. Voor n1

=

0,1,2,3, ..(t·(v,d)

=

16); c1

=

2;
tbv,o,c,sK(n1,c1)

=

{ 0, 64, 3840, 430080, 55910400, 7514357760, 991895224320, 124695399628800, 14589361756569600, 1556198587367424000, 148150105517378760000,
1.2282990566531767e+22, 8.598093396572237e+23, 4.867843646059359e+25, 2.0862187054540108e+27, 6.008309871707551e+28, 8.712049313975949e+29 }.

(6.5.3)

Totaal aantal varianten in alle subsets (per lengte) over nodes (leaves èn nesten):


Ten slotte kunnen de verzamelingen over de aantallen basislementen worden samengevoegd in een omvattende verzameling.

tbv,o,c,s*U

(v,d,c1): de verzameling van alle n1 verzamelingen

tbv,o,c,s*K

(n1,c1) bij c1 connectiefsymbolen.
{ v, d

|

n1 c1 (

tbv,o,c,s*K

(n1,c1)

tbv,o,c,s *U

(v,d,c1) )c1, n1 , d ,v }.

Omvang.


tbv,o,c,sU(v,d,c1): het totale aantal elementen in alle deelverzamelingen

tbv,o,c,s* K

(n1,c1) van

tbv,o,c,s*U

(v,d,c1).
Berekening analoog aan die van tcv,o,c,s*U(v,d ,c1) en van tbv,o,c,s*U(v,d,c1 ).
Bijv. Voor v

=

2; d

=

2;

tbv,o,c,sU

(v ,d,c1)

=

9.334237994986363e+29.

7.

 

Conclusie aangaande syntactische expansie.


Er zijn vele keuzes te maken in de manier waarop we syntactische variatie van proposities en redeneringen in een elementair logisch systeem kunnen afleiden en berekenen. Hierboven zijn enkele voorbeelden gegeven en hun resultaten. We laten hieronder een samenvatting volgen, beperkt tot de waarde tm v,o,c,s*U(v,d,c1): het totale aantal elementen in alle deelverzamelingen

tmv,o,c*K

(n1, c1) van

tmv,o,c,s*U

(v,d ,c1) die bestaan uit 'minimale' syntactische varianten over eindelementen en nesten binnen meerplaatsige geneste structuren met elk n1 unieke basiselementen, inclusief valentievarianten, volgordevarianten en connectiefvarianten bij c1 connectiefsymbolen onder de basale parameterwaarden v

=

2 en d

=

2.
(7.1)

Syntactische variatie bij symmetrische (meerplaatsige) connectieven. (3.) 


Bijv. Voor v

=

2; d

=

2; c1

=

4;
tmv,o,c,sU(v,d,c1 )

=

2.562518773558318e+37.
(7.2)

Syntactische variatie bij symmetrische connectieven - tot diepteniveau twee. (4.) 


Bijv. Voor v

=

2; d

=

2; c1

=

2;
tcv,o,c,sU(v,d,c1 )

=

1.1538146720234845e+23.
(7.3)

Syntactische variatie bij asymmetrische ( binaire) connectieven (5.)  .


Bijv. Voor v

=

2; d

=

2; c1

=

2;
tbv,o,c,sU(v,d,c1 )

=

9.334237994986363e+29.
(·) Theory of Subjective Conscousness - A zombie won't catch your consciousness.

C.P. van der Velde © 2014, 2018, 2023.