Alento
Training & Advies -
Arc of Essentials ©
- drs. C.P. van der Velde -
12-11-2015
Dimensie/ vakgebied:
Logica
Cursus / training: Methode Formele Logica
©
Introductie Predikatenlogica (PDL).
Uitgangspunten en richtlijnen.
I.
Opbouw van de predikatenlogica.
1.
Het kader van de predikatenlogica
Aanvullingen op de Propositielogica.
De predikatenlogica maakt het mogelijk om in redeneringen rekening te houden met waarheidsrelaties binnen
elementaire beweringen.
1.1.
Notaties.
1.1.1. Algemene notaties.
PDL : Predikatenlogica. Als formeel logisch systeem.
PDL* : De verzameling toegelaten uitdrukkingen (zinnen/ formules) van
PDL.
PDL-I : Predikatenlogica van de eerste orde. (Waarin geen predicaties over predicatie
s toegestaan zijn).
PDL-I* : De verzameling toegelaten uitdrukkingen (zinnen/ formules) van
PDL-I.
1.2.
Opbouw van predikaties.
In de predikatenlogica wordt gebruik gemaakt van predikaten, termen en kwantoren.
Deze dienen om meer specifieke betekenissen aan te geven binnen de semantische eenheden die in de
propositielogica als proposities bekend zijn.
Neem bijv. de zin:
Z: 'Jan slaat Piet met een hamer op zijn kop in de tuin als het regent bij de buren'.
Hoe zo'n zin in de PDL te vertalen zullen we hieronde r, met alle tussenstappen,
laten zien:
(1) Proposities en connectieven.
We benaderen de zin eerst vanuit het perspectief van de propositielogica ( PPL).
We brengen daarbij een onderscheid aan in elementaire beweringen ( atomen) en voegwoorden (
connectieven).
(a) Atomen.
Eerst de elementaire beweringen in de taal. De vormen de atomaire formules (oftewel de enkelvoudige
proposities) in de formele logica.
In zin Z hebben we er twee:
· A 1: 'Jan slaat Piet met een hamer op zijn kop in de tuin';
· A 2: 'het regent bij de buren'.
Dus hier hebben we de verzameling: ATM * = {A 1,A 2}.
(b) Connectieven.
De logische verbindingen tussen predicaties worden in het gewone spraakgebruik vaak gelegd
door voegwoorden (al s, da n, wan t, enz.). Die voegwoorden kunnen we in formele logica
vertalen naar de connectieven. De connectieven vormen de logische structuur van de formule
of redenering.
In zin Z hebben we de semantische structuur: Z: '(P1 ALS P2)'.
Het voegwoord 'als' kunnen we redelijk vertalen in de Implicatie. Daarmee kijgen we als logische structuur:
Z: '(P2  P1)'.
Alle wetten van de PPL zijn onverkort geldig in de PDL, maar de PDL
heeft wel aanvullende regels nodig.
(2) Predikaten en termen.
We maken vervolgens onderscheid tussen twee hoofdgroepen van grammaticale elementen binnen de
proposities.
(a) Predikaten.
De predikaten verwijzen (semantisch) naar eigenschappen en processen. Ze kunnen (syntactisch)
worden toegekend aan termen.
Het betreft begrippen zoals eigenschappen en werkwoorden, die niet verwijzen naar zelfstandige entiteiten.
In die zin zijn ze algemeen toepasbaar, c.q. 'abstract'. Symbolen voor predikaten: termini communes,
common nouns.
In de PDL vormen zij het draagvlak voor de predikaties, die tot de atomaire formules
behoren. Ze worden daarom met hoofdletters geschreven.
In zin Z hebben we: PDS* = {Slaan, Regenen}; of verkort: {S,R}.
(b) Termen (in engere zin).
De termen bestaan uit object-variabelen, constanten en logische functies. Dit zijn aanduidingen voor
elementen of delen van het betreffende domein: individuen of groepen. Ze verwijzen (semantisch)
naar individuen en groepen van objecten in een bepaald domein (bijvoorbeeld een populatie).
De objecten kunnen via object-variabelen en object-constanten (syntactisch) aan kwantoren
worden gebonden. Die laatste kunnen op hun beurt worden gebonden aan predikaten.
De object-constanten worden met kleine letters geschreven.
Hier:
TERM* = {jan, piet, hamer, kop, tuin, de-buren}; of verkort: {j,p
,h,k,t,b}.
(3) Het begrip predikatie
In de PDL kunnen eigenschappen en relaties via begrippen - predikaten en functies -
door de 'gebruiker' van het systeem naar eigen goeddunken worden toegekend aan objecten in het domein.
Het centrale instrument hierbij is predikatie.
(a) Het proces predikatie houdt in: eigenschappen worden aan dingen toegekend.
De enige beperking hierbij is dat dit alleen op zinvolle wijze kan wanneer de regels worden gevolgd
van de 'taal' van het systeem, de expressieregels of syntax.
(b) Het element predikatie heeft betrekking op een zelfstandige syntactische eenheid:
elke elementaire bewering bestaat - in de taal - uit minstens één predicatie, d.i. een stelling
dat iets een bepaalde eigenschap heeft.
(4) Codes voor predikatie.
'A(t)' : Predikaat A komt toe aan een domein-element of term (variabele, constante
of logische functie) met identificatiecode t.
' f(t)' : Functie f wordt toegepast op een domein-element of term
(variabele, constante of logische functie) met identificatiecode t.
(5) Definitie en referentie van predicaatnamen.
(a) Definitie (intention, (connotation).
De verzameling eigenschappen (attributen) die voor een object of individu moeten gelden wil het
predicaat daarop toepasbaar zijn.
(b) Referentie (extension, denotation).
De verzameling (veronderstelde!) objecten of individuen waarop het predicaat wordt toegepast
wegens hun (veronderstelde) eigenschappen (attributen).
(6) Hiërarchische ordening.
(·) Stamverzameling: genus.
Topverzameling, bovengrens: ( summum genus).
Bijv. 'ding' ( substantia), 'kwaliteit' of 'relatie'.
(·) Verdeling in deelverzamelingen: divisi.
(·) Deelverzameling: species (soort).
(·) Deelverzameling van deelverzameling: subspecies (Ondersoort).
(·) Onderscheidende eigenschappen van een species: differentia.
(·) Laatste ondeelbare eigenschap, ondergrens (infima species).
Verwijst nog naar onvervreemdbare, inherente, intrinsieke, 'essentiële' eigenschap.
Dit onderscheid is vaak louter theoretisch, hypothetisch c.q. zeer relatief, afhankelijk van arbitraire
definitie, formalisering, enz..
(7) Opbouw van predicaties.
Vervolgens kunnen we de predikaten en termen combineren tot predikaties. In PDL
-I kunnen deze niet genest worden en zijn dus enkelvoudige stellingen, oftewel elementaire beweringen.
Ze vormen een specificatie van de atomaire formules (oftewel de enkelvoudige proposities)
die we al afgebakend hadden.
Voor zin Z krijgen we:
· Pd1 : 'S door j, van p, met h, op
k, in t', of verkort: S(j,p,h,
k,t);
· Pd2 : 'R bij b', of verkort: R(b).
(8) De formule in PDL.
Zin Z kan nu in formule F worden omgezet door voegwoorden en predicaties met elkaar te verbinden:
F: '(R( b)  S( j, p,
h, k, t))'.
1.3.
Logische connectieven in PDL: kwantoren.
De kwantoren geven het bereik aan van de predikaten: syntactisch in termen van
object-variabelen binnen de argumentlijsten van predikaties; en semantisch in termen van
objecten binnen het (sub)domein.
Tabel 1.
Symbolen in Predikatenlogica (PDL): kwantoren
|
Kwantor
|
|
Uitdrukking in tekst
|
Logisch symbool
|
Symbool in tekst
|
Universele kwantor:
categorische bewering
|
|
'Voor ALLE ..'
|

|
|
Existentiële kwantor:
particuliere bewering
|
|
'Voor SOMMIGE ..'
|
 , ,
 [ [≥1]
|
%
|
Uniekheids kwantor,
singuliere bewering:
|
|
'Voor PRECIES ÉÉN ..'
|
 [ [=1],
 !
|
%(=1),
%!
|
Minimum kwantor,
ondergrens:
|
|
'Voor MINSTENS k ..',
'Voor MEER DAN (k-1) ..'
|
 [ [≥k]
|
%(≥=k)
|
Maximum kwantor,
bovengrens:
|
|
'Voor HOOGSTENS k ..',
'Voor MINDER DAN (k+1) ..'
|
 [ [≤k]
|
%(≤=k)
|
Numerieke kwantor,
kwantitatieve bewering:
|
|
'Voor PRECIES k ..'
|
 [ [=k]
|
%(=k)
|
|
Symbool in Modeltheorie
|
|
|
|
|
Structuur,
datastructuur voor het domein.
|
|
'STRUCTURE'
|
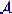
|
A!
|
Assignment,
'bedeling', toekenning van variabelenamen aan domeinelementen.
|
|
'ASSIGNMENT'
|
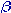
|
B!
|
2.
Syntax voor Predikatenlogica.
Uitbreiding van de PPL.
2.1.
Het alfabet van PDL.
De verzameling symbolen van PPL.
(1) De logische symbolen van PDL.
Regels (1a) tot en met (1f) zijn identiek als voor PPL.
Specifiek voor PDL gelden.
(1g) Logische kwantoren (kwantifiers).
Q * : verzameling toepasbare kwantoren.
Q * = {  ,
 ,  !' }.
Qsub> *( E) : verzameling voorkomende kwantoren - in expressie(s) E.
Q
( E) : aantal voorkomende (toegepaste) kwantoren - in expressie(s) E.
QU
( E) : aantal voorkomende (toegepaste) Universele kwantoren - in expressie(s) E.
QE
( E) : aantal voorkomende (toegepaste) Existentiële kwantoren - in expressie(s) E.
(1h) Variabelenamen.
Object variabelen: willekeurige eenheden (objecten) uit het domein.
VAR* : verzameling toepasbare variabelenamen.
VAR* = {'x', 'y', 'z', ..
'u', 'v', 'w', .. }; = {v[1]
, .., v[n] }.
VAR*(E) : verzameling voorkomende variabelenamen - in expressie(s)
E.
VAR
(E) : aantal voorkomende variabelenamen - in expressie(s) E.
(1i) Kwantiteit, generaliteit.
Omvang van het semantisch bereik van een expressie.
' Q!(E)' : (relatieve) kwantiteit - van expressie(s) E.
(1j) Referentiële selectie.
Inhoud van het semantisch bereik van een expressie.
' R*(E)' : referentiegebied, referentieel bereik, referentiële
verzameling, selectie, (sub)domein - van expressie(s) E.
'R!(E)' : omvang van referentiële verzameling, selectie, (sub)domein - van
expressie(s) E.
Een referentiegebied van E, R*( E): bevat alle grondinstanties van
E,
in alle mogelijke combinaties volgens de connectiefstructuur van E,
in een lijst naar omvang van het gekozen (sub)domein D[m]·
n.
'  ( (ref)', ' 
ref' : Equivalentie in termen van referentieel bereik.
(1k) Aantal voorkomens (prevalentie, occurances).
'OCC(E1, E2 )' : aantal voorkomens van (dezelfde) expressie(s) E2 - in expressie(s)
E1.
'OCC(E, t )' : aantal voorkomens van (dezelfde) term(en) t - in
expressie(s) E.
(1l) Argumentplaatsen (ariteit).
ARY(S) : aantal argumentplaatsen (ariteit) - van symbool S (
functieterm of predicaat).
(1m) Argumenten.
ARG*(E) : verzameling voorkomende (toegepaste) argumenten - in expressie(s) E.
ARG
(E) : aantal voorkomende (toegepaste) argumenten - in expressie(s) E.
(1n) Vrije variabele(n).
Een vrije variabele is niet aan een kwantor gebonden, d.w.z. ligt binnen een bepaalde syntactische context
buiten de scope van een kwantor.
'FREE(F, x )' : variabele(n) x is/zijn 'vrij' - in formule(s) F.
'FREE
*(F)' : verzameling van voorkomende niet-kwantor-gebonden variabelen - in formule(s)
F.
(1o) Codes voor type afleiding.
Speciale notaties:
(1o1) Algemene substitutie.
Vervanging van een expressie (formule, predicatie of term).
:= : substitutie operator.
sbs() : een substitutie functie.
sbs[ i] : een specifieke substitutie operatie.
'  (s) (s)' : Equivalentie onder substitutie.
'  (s) (s)' : Implicatie onder substitutie.
(1o2) Variabele-hernoeming (renaming), c.q. herindexering (permutatie).
'  (v) (v)' : Equivalentie onder variabelen-hernoeming.
'  (v) (v)' : Implicatie onder variabelen-hernoeming.
(1o3) Argument-instantiatie.
Verlaging van de generaliteit van een term, via substitutie: insertie van een meer specifiek element (
instantiatie).
ins() : een subsumptie functie.
ins[ i] : een specifieke subsumptie operatie.
'  (i) (i)' : Implicatie onder argument-instantiatie.
(1o4) Argument-subsumptie.
Verlaging van de generaliteit van een term, via referentiële onderschikking ( subsumptie).
ssm() : een subsumptie functie.
ssm[ i] : een specifieke subsumptie operatie.
'  (ssm.) (ssm.)' : Implicatie op grond van subsumptie.
(1o5) Argumenten-unificatie.
Bewerkstelligen van uniformiteit van (minstens) twee expressies c.q. termen.
' Most general unifier' (MGU): argumenten-unificatie op een aantal expressies
met maximaal behoud van referentieel bereik, dus logische kracht.
mgu() : een most general unifier substitutie functie.
mgu[ i] : een specifieke most general unifier substitutie operatie.
'  (u) (u)' : Equivalentie onder argumenten-unificatie.
'  (u) (u)' : Implicatie onder argumenten-unificatie.
'  (mgu) (mgu)' : afleiding onder argumenten-unificatie,
met (uitsluitend) most general unifier.
(2) De niet-logische symbolen van PDL.
(2a) Objectnamen, constanten.
Of nul-plaatsige logische functies.
Voor unieke eenheden (objecten) uit het domein.
CNS* : verzameling toepasbare object constanten (d.i. nul-plaatsige functie
s).
CNS* = {'a', 'b', '
c', 'd', 'e', .. }; =
{c[1], .., c[n] }.
'c', 'cd' : een 'normale' (bestaande) 'domein' constante
).
'cs' : een ad hoc ingevoerde (virtuele) Skolem
constante.
CNS*(E) : verzameling voorkomende constanten - in expressie(s) E
.
(2b) Functienamen.
Of meerplaatsige logische functies.
Voor selecties of bewerkingen van eenheden (objecten) uit het domein.
FNC* : verzameling (één- of meerplaatsige) functies.
FNC* = {'f', 'g', '
h', .. }; = {f[1],
.., f[n] }.
'f(x)', 'fd(x)' : een 'normale' (bestaande) '
domein' functie.
'fs(x)' : een ad hoc ingevoerde (virtuele)
Skolem constante.
FNC*(E) : verzameling voorkomende functies - in expressie(s) E.
(2c) Predikaatnamen.
Voor eigenschappen van eenheden (objecten) uit het domein, waaronder relaties.
PDC* : verzameling predikaten.
PDC* = {'A', 'B', 'C', ..
'P', 'Q', 'R', .. }.
= {A[1], A[2], .. A[n] }.
PDC*(E) : verzameling voorkomende predikaatnamen - in expressie(s)
E.
2.2.
Formatieregels voor formules in PDL.
Vereisten voor syntactische welgevormdheid van syntactische constructies - formules en expressies -
in PDL.
2.2a. Formatieregels voor termen (in PDL).
' wft' : een welgevormde term ( well-formed term).
Inductieve definitie van wft's in PDL.
(1) Als x een object variabele is, dan is 'x' een wft.
(2) Als c een object constante is, dan is 'c' een wft.
(3) Als f·n een n-plaatsig functie symbool is, en {
t[1], .., t[n]} zijn wft's
,
dan is 'f·n(t[1], ..,
t[n])' een wft (recursief in PDL).
(4) Niets anders is een wft in PDL.
WFT* : verzameling toepasbare welgevormde termen.
WFT*(E) : verzameling voorkomende welgevormde termen - in expressie(s)
E.
2.2b. Formatieregels voor formules (in PDL).
' wff' : een welgevormde formule ( well-formed formula).
Inductieve definitie van wff's in PDL.
(1) Als F een wff is in PPL, dan is ' F' ook een wff in
PDL.
(2) Als P ·n een n-plaatsig predicaat symbool is, en { t
[1], .., t[n]} zijn wft' s,
dan is ' P·n( t[1], .., t
[n])' een wff ( niet recursief) in PDL-I).
(3) Als F een wff is en x is een object variabele,
dan zijn '  x F x F' en en '  x F
x F' wff's (recursief).
(4) Als { t[1], .., t[n]} zijn
wft' s,
dan is ' t[1] = .. t[n
]' een wff in PDL.
(5) Niets anders is een wff in PDL.
WFF* : verzameling toepasbare welgevormde formules.
WFT*(E) : verzameling voorkomende welgevormde formules - in expressie
(s) E.
2.3.
Het bereik (de scope) van kwantoren in formules.
Het bereik van een kwantor wordt aangeduid met behulp van '( .. )':
Notaties.
SCOPE(F, Q[i]) : scope van kwantificatie Q[i] in formule F
.
(invoer is formule F en i-de kwantificatie-vermelding Q[i] in F, Een
Q[i] bestaat uit kwantor-naam en j-de variabele-naam in F,
uitkomst is subformule van F).
QU(F, x[i] )' : variabele x[i] ligt in formule F
binnen de scope van een universele kwantor.
QU(F, x[i] )' : variabele x[i] ligt in formule F
binnen de scope van een existentiële kwantor.
2.4.
Vrije variabelen in wff formules.
Een vrije variabele x in een formule F is (syntactisch) niet gebonden aan een kwantor
in F, d.w.z. ligt buiten de scope van enige kwantor in F.
De vermelding van een vrije variabele x in een formule F betekent (semantisch)
in het algemeen zoiets als 'gegeven een variabele x'.
De nadere interpretatie is afhankelijk van de vraag of F in een grotere context
voorkomt.
(1) Als F voorkomt in het bereik van minstens één kwantor binnen een meeromvattende formule, zeg
G, dan betekent het zoiets als 'gegeven de eerder vermelde variabele x'. In dat geval dient x
hetzij universeel, hetzij existentieel te worden geïnterpreteerd.
(2) Zoniet, dan mag x universeel worden geïnterpreteerd.
(¬(' x'  FREE *( A ) )
 ({  x A x A } ≡ A
).
(¬(' x'  FREE *( B ) )
 ({  x x ( A( x)
 B B) } ≡ ((  x A x A
( x) )  B B) ).
2.5.
Afsluiting (closure) van wff formules.
Een afsluiting van een wff formule F in PDL bestaat in het binden
van elke vrije variabele in F aan een bepaalde kwantor Q.
SENT(F), Fc := CLOSE(F) : een afsluiting
van wff formule F.
Een gesloten wff formule wordt een zin ( sentence) genoemd.
(a) Het type kwantor voor een afsluiting kan zijn existentieel (QU) of universeel (QU).
(b) De keuze van het type kwantor voor een afsluiting wordt ingegeven door semantische overwegingen:
met name de keuze van interpretatie. Een afsluiting vertegenwoordigt dus
een nadere interpretatie van de formule.
(c) Elke afsluiting is dus afhankelijk van keuzes van het type van toe te voegen kwantificaties.
Daardoor is ze een afgeleide van de oorspronkelijke formule. Er is dus géén unieke afsluiting per
formule.
(d) De plaats van de kwantor dient met de betreffende variabele vooraf te gaan aan alle predicatie(s)
met die variabele: (1) hetzij onmiddellijk (2) hetzij via tussenliggende nesting(s) waardoor die predicatie(
s) binnen het bereik van de betreffende kwantor liggen.
2.6.
Vuistregels voor efficiënte formuleringen in PDL
.
(·) Houd het aantal kwantoren in een formule zo klein mogelijk.
(·) Houd het bereik van kwantoren in een formule zo beperkt mogelijk.
(·) Houd kwantoren in een formule zo dicht mogelijk bij de predicaties waarop ze betrekking hebben.
II.
Basiswetten in de predikatenlogica.
3.
Kwantificatie over predicaties.
3.1.
Effecten van kwantificatie op predicaties
.
Kwantificatie bepaalt het bereik van variabelen. Dit betekeniseffect geldt zowel op syntactisch niveau
als op semantisch niveau, zij het op heel verschillende wijze.
(a) Syntactisch:
Door kwantificatie kunnen variabelesymbolen in formules in een logische taal worden gebonden
- in de 'lineaire' syntactische structuur - aan bepaalde kwantorsymbolen. Daarmee krijgen de
kwantorsymbolen een bereik over de rechts volgende predicaties waarin de betrokken variabelen voorkomen.
Dit bereik kan eenvoudig begrensd worden door begrenzingssymbolen, zoals '(', ')'.
(b) Semantisch:
Door kwantificatie kunnen variabelenamen in het lexicon van een logische taal worden gebonden
- in de 'non-dimensionale' semantische structuur - aan specifieke selecties van objecten
in een domein buiten die logische taal. Daarmee kunnen naar willekeur eigenschappen en relaties via
predicaten worden toegekend aan die objecten. Vervolgens kunnen de logische wetten worden toegepast
om te kijken hoe die eigenschappen en relaties met elkaar combineren en al dan niet mogelijke of zelfs ware
domeintoestanden opleveren.
3.2.
Typen van predicaties naar hun kwantortype.
Codes voor kwantificering.
Hieronder volgen eerst de elementaire vormen van gekwantificeerde predicaties met hun afgeleide propositie
vormen, [ zowel de expliciete als impliciete ( Skolem) vormen. ]
3.2.1. Standaard kwantor typen.
3.2.1.1.
Universele kwantor.
(·) Universele kwantor - definitie.
De universele kwantor dient voor de verwijzing van een argument x naar èlk element c.q.
object d[i] uit het betreffende (sub)domein D[m]
·n.
'  ', '
' : Universele kwantor.
'  x x <..>' betekent:
'Voor èlk element x (uit het domein) geldt <..>',
en/of 'Voor àlle elementen x (uit het domein) geldt <..>'.
(·) Universeel gekwantificeerde predicatie.
Zgn. ' Gamma' formule.
Geplaatst voor een predikatie met argument x betekent dit dus dat het betreffende predikaat via
argument x van toepassing is op al die elementen.
Bijv.: '  x x A( x)': 'Elk ding x is A'.
(·) Universele kwantor als domein-selector.
Universele kwantor impliceert onder de gerelateerde variabelenaam de volledige verzameling domeinobjecten.
Dat impliceert dat die predikatie in Conjunctie geldt over dat gehele (sub)domein.
Betekent voor domeinen met omvang van n individuen:
Bijv.: {  x x A( x) }:
genoteerd:
 ( n | (A(x [1])
 A(x [2])  ..
A(x [n]) ) ).
Of, genoteerd ( isomorf) in PPL:
 (iso) (iso)PPL ( n
| (A 1  A 2
 .. A n) ).
Of, genoteerd als (ongeordende) verzameling:
 ( n | {A(x [1]) ,A(x [2]
) .. ,A(x [n]) } ).
Of, met prefix notatie:
 ( n |
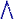 (i:=1, (i:=1, ..n) A(x [
i]) ).
En representeert bij n objecten a [i] een domeinselectie met de datastructuur:
 ( (ref) ( n | (A(
d [1])  A(d [2]) 
.. A(d [n]) ) ).
(zgn. Herbrand conjunction).
Of, met simpeler notatie:
 ( (ref) ( n | {A(
d [1] + d [2] + .. d [n]) } ).
Of, kort en praktisch:
 ( (ref) ( n | {A
1, A 2, .. A n } ).
(·) Universele kwantor als connectief-selector.
De universele kwantor treedt typisch op met betrekking tot een Implicatie als eerste (sub
)connectief:
Bijv.: '  x x (A( x)  B(
x))':
'Voor ALLE dingen x geldt DAT (ALS het een A is, DAN is het ook een B)'.
Bijv.: '  x x (Z( x)  V(
x))': 'Alle zwanen zijn vogels';
of: 'Voor alle x geld t, dat (ALS x zwaan is, DAN is x een voge l)'.
3.2.1.2.
Existentiële kwantor.
(·) Existentiële kwantor - definitie.
De Existentiële kwantor dient voor de verwijzing van een argument x naar énig element c.q.
object d[i] uit het betreffende (sub)domein D[m]
·n.
'  ', ' %' : Existentiële kwantor.
'  x x <..>' betekent:
' Er is een element x (uit het domein) waarvoor geldt dat <..>',
en/of 'Voor minstens één element x (uit het domein) geldt <..>',
en/of 'Voor sommige elementen x (uit het domein) geldt <..>'.
en/of 'Voor énig element x (uit het domein) geldt <..>'.
(·) Existentieel gekwantificeerde predicatie.
Zgn. ' Delta' formule.
Geplaatst voor een predikatie met argument x betekent dit dus dat het betreffende predikaat via
argument x van toepassing is op sommige van die elementen.
Bijv.: '  x x A( x)': 'Er is een ding x dat is A', of
'Énig ding x is A'.
(·) Existentiële kwantor als domein-selector.
Existentiële kwantor impliceert onder de gerelateerde variabelenaam een (niet-lege) selectie van
disjuncte domein-objecten.
Dat impliceert dat die predikatie in Disjunctie geldt over dat gehele (sub)domein.
Betekent voor domeinen met omvang van n individuen:
Bijv.: {  x x A( x) }:
genoteerd:
 ( n | (A(x [1])
 A(x [2])  ..
A(x [n]) ) ).
Of, genoteerd ( isomorf) in PPL:
 (iso) (iso)PPL ( n
| (A 1  A 2
 .. A n) ).
Of, met prefix notatie:
 ( n |
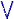 (i:=1, (i:=1, ..n) A(x [
i]) ).
En representeert bij n objecten a [i] een domeinselectie met de datastructuur:
 ( (ref) ( n | (A(
d [1])  A(d [2]) 
.. A(d [n]) ) ).
(zgn. Herbrand disjunction).
Of, met simpeler notatie:
 ( (ref) ( n | {A(
d [1] /d [2] .. /d [n]) } ).
Of, kort en praktisch:
 ( (ref) ( n | {A
1 /A 2 .. /A n } ).
(·) Existentiële kwantor als connectief-selector.
De existentiële kwantor treedt typisch op met betrekking tot een Conjunctie als eerste (sub
)connectief:
Bijv.: '  x x (A( x)  B( x
))':
'Voor SOMMIGE dingen x geldt DAT (x is A, EN tegelijk B).
Bijv.: '  x x (Z( x)  W( x
)': 'Er bestaan witte zwanen';
of: 'Er bestaat minstens één object x dat zwaan is en tegelijk wit'.
Universeel - Existentieel kwantor conversie.
(·) Universeel naar Existentieel conversie.
Bijv.: {(¬  x x A( x))
 (  x x ¬A( x)) };
 ( (ref) (¬(A(d [1])
 A(d [2])  ..
))  (¬A(d [1])  ¬A(d
[2])  .. ) );
 ( (iso) (¬(A 1
 A 2  .. ))
 (¬A 1  ¬A 2
 .. ) );
 ( (Sk+1) ((¬
 x x A( x))  ¬A(
cd) ).
Bijv.: {(  x x ¬A( x))
 (¬  x x A( x)) };
 ( (ref) ((¬A(d [1])
 ¬A(d [2])  ..
))  ¬(A(d [1])  A(d
[2])  .. ) );
 ( (iso) ((¬A 1
 ¬A 2  .. ))
 ¬(A 1  A 2
 .. ) );
 ( (UI) (¬A( x)
 (¬  x x A( x)) ).
Bijv.: {(  x x A( x)) 
(¬  x x ¬A( x)) };
(·) Existentieel naar Universeel conversie.
Bijv.: {(¬  x x A( x))
 (  x x ¬A( x)) };
 ( (ref) (¬(A(d [1])
 A(d [2])  ..
))  (¬A(d [1])  ¬A(d
[2])  .. ) );
 ( (iso) (¬(A 1
 A 2  .. ))
 (¬A 1  ¬A 2
 .. ) );
 ( (UI) (¬
 x x A( x))  ¬A( x
) ).
Bijv.: {(  x x ¬A( x))
 (¬  x x A( x)) };
 ( (ref) ((¬A(d [1])
 ¬A(d [2])  ..
))  ¬(A(d [1])  A(d
[2])  .. ) );
 ( (iso) ((¬A 1
 ¬A 2  .. ))
 ¬(A 1  A 2
 .. ) ).
 ( (Sk+1) (¬A( cd
)  (¬  x x A( x
)) ).
Bijv.: {(  x x A( x)) 
(¬  x x ¬A( x)) };
 ( (Sk+1) (A( cd
)  (¬  x x ¬A( x
)) );
3.2.2.
Non-standaard kwantor typen:
Singulier, Minimum, Maximum, en Numeriek.
3.2.2.1.
Singuliere kwantor.
(·) Singuliere kwantor - definitie.
De Singuliere kwantor dient voor de aanduiding van uniciteit: de verwijzing van een argument x
naar precies één element c.q. object d[i] uit het betreffende (sub)
domein D[m]·n.
'  [ [=1]', ' 
!', ' %!', '1 !' : Singuliere kwantor.
'  [ [=1]x <..>' betekent:
'Voor precies één element x (uit het domein) geldt dat <..>',
en/of 'Voor één element x (uit het domein) geldt <..>'.
en/of 'Voor 1 element x (uit het domein) geldt <..>'.
(·) Singulier gekwantificeerde predicatie.
Geplaatst voor een predikatie met argument x betekent dit dus dat het betreffende predikaat via
argument x van toepassing is op precies één van die elementen.
Bijv.: '  [ [=1]x A( x)': '
Precies één ding x is A',
of 'Één ding x is A'.
of ' 1 ding x is A'.
(·) Singuliere kwantor als domein-selector.
De singuliere kwantor impliceert onder de gerelateerde variabelenaam een (niet-lege) selectie van
exclusief-disjuncte domein-objecten.
Dat impliceert dat die predikatie in exclusief-Disjunctie geldt over dat gehele (sub)domein.
Betekent voor domeinen met omvang van n individuen:
Bijv.: {  [ [=1]x A( x) }:
 ( n | (A(x [1]) #
A(x [2]) # .. A(x [n]) ) ).
En representeert bij n objecten a [i] een domeinselectie met de datastructuur:
 ( (ref) ( n | (A(
d [1]) # A(d [2]) # ..
A(d [n]) ) ).
'Er is precies één ding x zodat A( x)'.
Het betekent dus dat er naast x geen dingen y zijn die A zijn en tegelijk niet identiek aan
x.
Bijv.: {  [ [=1]x A( x) };
 ((  x x A( x))
 (  x x
 y y ((A( x)  A( y))
 ( x=y))));
 ((  x x A( x))
 (  x x
 y y (A( x)  (A( y)
 ( x=y)))));
 (  x x (A( x)
 (  y y (A( y)
 ( x=y)))));
 (  x x (A( x)
 (  y y (A( y)
 ( x=y)))));
 (  x x
 y y (A( y)  ( x
=y))).
(Bijv.'Er is slechts één Paus').
(·) Singuliere kwantor als connectief-selector.
De singuliere kwantor treedt typisch op met betrekking tot een Conjunctie als eerste (sub
)connectief:
Bijv.: '  [ [=1]x (A( x)
 B( x))':
'Voor 1 ding x geldt DAT (x is A, EN tegelijk B).
Bijv.: '  [ [=1]x (P( x)
 A( x)': 'Er bestaat één planeet aarde';
of: 'Er bestaat precies één object x dat planeet is en tegelijk (de) aarde'.
(Meer precies is natuurlijk: ..
planeet die mensen op aarde gewoonlijk aanmerken als (de) 'aarde').
(·) Afleidbaarheid:
Een singulier gekwantificeerde predicatie zoals '  [ [=
1]x A( x)' is door haar exclusiviteit nooit afleidbaar uit bijv. '
 x x A( x)', maar ook niet uit bijv. 'A( c)'
(want daarnaast kan bijv. voorkomen 'A( d)', etc.).
Een singulier gekwantificeerde predicatie kan, meer algemeen, niet afgeleid zijn van
een 'sterkere' predicatie (met hogere generaliteit en/of zekerheid).
(·) Afgeleide(n):
Uit een singuliere predicatie is wel een zwakkere kwantificatie afleidbaar, dus met degressie:
nl. een existentiële.
Via operatie: Disjunctieve expansie.
Bijv.:
{ !x A(x) ) };
 ( (degres) (
 x x A( x) );
Non-standaard kwantor typen:
Minimum en maximum.
Interval grenzen, extremen, limieten ( interval limits, bounderies, borders).
Comparatieve modificatie.
3.2.2.2.
Minimum.
' Minstens': ondergrens of minimumwaarde.
Eenvoudige vorm.
(1) ' Minstens (≥) één ding is A':
 (  x x A( x) ).
(2) ' Minstens (≥) twee dingen zijn A'
(' Meer dan één ding is A')
('Er zijn minstens (&ge) twee dingen zodat A( x)'):
 (  x x
 y y (A( x)  A( y)
 ¬( x=y)) ).
(3) ' Minstens (≥) drie dingen zijn A:
(' Meer dan twee dingen is A')
 (  x x
 y y  z z (A( x)
 A( y)  A( z)
 ¬( x=y) 
¬( x=z)  ¬( y=z
)) ).
Bijv.: 'Chris bezit meer dan twee auto's'.
D.w.z. 'Chris bezit minstens drie auto's'.
M.a.w.: 'Chris (c) bezit (B) meer dan twee auto's (A)'.
 (  x x
 y y (A( x)  A( y)
 B( c, x)  B(
c, y)  ¬( x=y)) ).
Bijv.: 'Er is een dokter (D) anders dan (dokter) Chris (c) die minstens één auto (A) bezit (B) '.
 (D( c)  (
 x x ((D( x)  ¬( x=
c))   y y (A( y)
 B( x, y)) )) ).
Meer algemene vorm.
'Er kunnen k (verschillende) samples van (verschillende) dingen x A zijn'.
 ( k |  (i
(i :=1, ..k) (  xi
xi A(x [i]) x ) i k
);
 ( k |  (i
(i :=1, ..k) A( cs
[i]) i, k );
Maar: verschillende samples kunnen hier dezelfde variabelewaarden bevatten.
Dus deze samples kunnen 'in werkelijkheid' onderling in samenstelling (d.i. semantisch)
geheel of gedeeltelijk samenvallen.
'Er kunnen k (verschillende) dingen x A zijn'.
 ( k |  (i
(i :=1, ..k) (  [
[=1]x[i] A(x [i]) x,
i ) k );
Maar: verschillende variabelenamen x kunnen in het algemeen verwijzen naar dezelfde waarde
(c.q. hetzelfde referentiële object in een domein).
Dus verschillende variabelenamen x[i] kunnen onderling in waarde (d.i.
semantisch) geheel of gedeeltelijk samenvallen.
' Minstens k dingen x zijn A'.
'Er zijn minstens k ( unieke) dingen x A'.
'Er zijn niet minder dan k dingen A'.
'Er zijn meer dan ( k-1) dingen A'.
D.w.z. met uitsluiting van mogelijke 'dubbelen' binnen de reeks.
 {  [ [≥
k]x A( x) ) };
 ( k |  (i
(i :=1, ..k) (  [
[=1]x[i] (A(x [i])
 (  j j ((1 ≤
j ≤ k)  (A(x [j])
 (¬( i = j)
 ¬(x [i] = x [j]) ) )
) j ) ) x ) i, k );
Surjectieve functie (surjectie):
('[afbeelding ..] op domein ..').
'Elke y heeft een x'.
Elke y is een afbeelding van minstens één origineel x.
Voor elke afbeelding / afgeleide y is er minstens één origineel x zodat R( x,
y) geldt.
M.a.w. Er zijn geen y waarvoor geen x zijn.
(Er kunnen wel y zijn waarvoor meerdere x zijn).
 {  y y
 x x (R( x, y)  (
 z z (R( x, z)  ( y
=z) ) z) ) y,x }.
 {  y y
 x x ( y = f( x)) }.
Dus:
Toegestaan is: {( x1, y1),( x2, y1), ..}.
Niet toegestaan is: {( x1, y1),( x2, y1), ( y2), ..}.
Bijv. f : R  R ; f(
x) = 2*x +1.
Bijv. f : R  [0,∞> ; f(
x) = abs( x).
Bijv. f : R  [0,∞> ; f(
x) = x**2.
Meer dan ...
'Er zijn meer dan k dingen A'.
Impliceert: 'Er zijn minstens ( k+1) dingen A'.
 {  [ [>
k]x A( x) ) };
 (  [ [≥
k+1]x A( x) );
 ( k |  (i
(i :=1, ..(k+1)) (
 [ [=1]x[i] (A(x
[i])
 (  j j ((1 ≤
j ≤ ( k+1))  (A(x [j])
 (¬( i = j)
 ¬(x [i] = x [j]) ) )
) j ) ) x ) i, k );
Bijv.: 'Aad bezit meer citroenen dan Dirk'.
 {(  k1 k1
 k2 k2 (  [ [=
k1]x (C( x)  B( a, x) )
x )
 (  [ [=k2]
y (C( y)  B( d, y) ) y
)
 ( k1 > k2) ) k2,
k1 }.
 {(  k1 k1
 k2 k2 ((A 1( a)
 (  [ [=k1]
x (C( x)  B( a, x) ) x
)
 (A 1( d)  (
 [ [=k2]y (C( y)
 B( d, y) ) y )
 ( k1 > k2) ) k2,
k1 }.
De meeste ...
Bijv.: 'De meeste A zijn B'.
 (  n n
 [ k] x ( k > ( n /2)) (A(
x)  B( x)) ).
3.2.2.3.
Maximum.
' Hoogstens': bovengrens of maximumwaarde.
Eenvoudige vorm.
(1) ' Hoogstens (≤) één ding is A'
Impliceert: ' Minder dan (<) 2 dingen zijn A( x)':
(M.a.w.: 'Als het predicaat 'A' op twee dingen wordt toegepast, dan zijn die dingen hetzelfde').
(Bijv. 'Er is hoogstens één Paus'):
 (  x x
 y y ((A( x)  A( y))
 ( x=y)) );
 (  x x
 y y (A( y)  ( x
=y)) ).
(2) ' Hoogstens (≤) 2 dingen zijn A( x)':
Impliceert: ' Minder dan (<) 3 dingen zijn A( x)':
 (  x x
 y y  z z ((A( x)
 A( y)  A( z))
 (( x=y)  (
x=z)  ( y=z
))) ).
Meer algemene vorm.
' Hoogstens k dingen x zijn A'.
'Er zijn hoogstens k ( unieke) dingen x A'.
'Er zijn niet minder dan k ( unieke) dingen x A'.
'Er zijn minder dan ( k+1) dingen A'.
D.w.z. met uitsluiting van mogelijke instanties/exemplaren buiten de reeks.
 {  [ [≤
k]x A( x) ) };
 ( k |  (i
(i :=1, ..k) (  [
[=1]x[i] (A(x [i])
 (  h h (( h >
k)  (¬  A(x [h]
) ) ) h ) ) x ) i, k );
 ( n, k |
 (i (i :=1, ..k)
(A(x [i])
 (  h h (( k <
h ≤ n)  (¬
 A(x [h]) ) ) h ) ) x
) i, k );
(Waarbij n de omvang van het referentiële domein is.
Indien dit een 'open' domein is, dan is n minstens aftelbaar oneindig, m.a.w. dan geldt (
n ≥  ) ).
Injectieve functie (injectie):
(eenduidige afbeelding', één-op-één afbeelding').
Elke afbeelding / afgeleide y heeft hoogstens één (dus uniek) origineel x.
Elke y is een afbeelding van hoogstens één origineel x.
Voor elke afbeelding / afgeleide y is er hoogstens één origineel x zodat R( x,
y) geldt.
Dus: Er zijn geen y waarvoor meerdere x zijn.
M.a.w. Er zijn geen x die naar dezelfde y gaan.
Niet elke afbeelding / afgeleide y hoeft per sé minstens één origineel x te hebben.
M.a.w. Er kunnen y zijn waarvoor geen x is.
Elk tweetal verschillende originelen/ elementen x
heeft een tweetal verschillende beelden/ elementen y.
 {  x x
 y y (R( x, y)  (
 w w (R( w, y)  ( x
=w) ) w) ) y,x }.
 {  x x1
 x x2 ( ( f( x1) = f
( x2))  ( x1 = x2))}.
Dus:
Toegestaan is: {( x1, y1),( x1, y2), ..}.
Toegestaan is: {( x1, y1),( x1, y2), ( y3), ..}.
Niet toegestaan is: {( x1, y1),( x1, y2), ( x3), ..}.
Niet toegestaan is: {( x1, y1),( x2, y1), ..}.
Bijv. f : R  R;
f( x) = 2*x.
Bijv. f : R  R;
f( x) = 2*x +1.
Minder dan ...
'Er zijn minder dan k dingen A'.
Impliceert: 'Er zijn hoogstens ( k-1) dingen A'.
 {  [ [<
k]x A( x) };
 (  [ [≤
k-1]x A( x) );
 ( k |  (i
(i :=1, ..(k-1)) (
 [ [=1]x[i] (A(x
[i])
 (  h h (( h ≥
k)  (¬  A(x [h]
) ) ) h ) ) x ) i, k );
Bijv.: 'Ed bezit minder fietsen dan Ger'.
 {(  k1 k1
 k2 k2 (  [ [=
k1]x (F( x)  B( e, x)
x )
 (  [ [=k2]
y (F( y)  B( g, y) y
)
 ( k1 < k2) ) k2,
k1 }.
 {(  k1 k1
 k2 k2 ((A 1( e)
 (  [ [=k1]
x (F( x)  B( e, x) x
)
 (A 1( g)  (
 [ [=k2]y (F( y)
 B( g, y) y )
 ( k1 < k2) ) k2,
k1 }.
De minste ...
Bijv.: 'De minste A zijn B'.
 (  n n
 [ k] x ( k < ( n /2)) (A(
x)  B( x)) ).
3.2.2.4.
Numerieke kwantor.
(·) Numerieke kwantor - definitie.
De Numerieke kwantor dient voor de verwijzing van een argument x naar ( minstens) k
elementen c.q. objecten d[i] uit het betreffende (sub)domein D
[m]·n.
'  [k] [k]', '  [ [
=k]', ' %[k]' : Numerieke kwantor.
'  [k]x [k]x <..>' betekent:
'Voor ( minstens) k elementen x (uit het domein) geldt <..>'.
'  [ [=k]x <..>' betekent:
'Voor precies k elementen x (uit het domein) geldt <..>'.
(·) Numeriek gekwantificeerde predicatie.
Geplaatst voor een predikatie met argument x betekent dit dus dat het betreffende predikaat via
argument x van toepassing is op [precies] k van die elementen.
Bijv.: '  [k]x [k]x A( x)': '( Minstens)
k dingen x zijn A'.
Bijv.: '  [ [=k]x A( x)': '
Precies k dingen x zijn A'.
(·) Numerieke kwantor als domein-selector.
De numerieke kwantor impliceert onder de gerelateerde variabelenaam een (niet-lege) selectie van
conjuncte domein-objecten.
Dat impliceert dat die predikatie in Conjunctie geldt over het geheel of een deelverzameling van
het betreffende (sub)domein.
Betekent voor een domein met omvang van n individuen:
Bijv.: {  [k]x [k]x }:
[  =ref ( n
, k, ((1 ≤ k ≤ n) | {
 (i (i :=1,..k) d [i
] } ) k,n );
=ref ( n, k, ((1 ≤
k ≤ n) | C [h]·k
) k,n ) ) h }.
Bijv.: {  [k]x [k]x A( x) }:
 ( n, k, ((1 ≤ k
≤ n) | {  (i (i
:=1,..k) A(d [i] ) } ) k,n ).
(·) Numerieke kwantor als connectief-selector.
De numerieke kwantor treedt typisch op met betrekking tot een enkelvoudige Literaal of een Conjunctie
als eerste (sub)connectief.
Bijv.: '  [k]x [k]x A( x)':
'Voor k dingen x geldt DAT ze A zijn'.
Bijv.: '  [3]x [3]x (B( j, x)
 A( x) )'.
'Jan bezit drie auto's'.
Meer algemene vorm.
'Er zijn precies k dingen x A'.
' Precies k dingen x zijn A'.
(·) Met uitsluiting van mogelijke 'dubbelen' binnen de reeks.
(·) Met uitsluiting van mogelijke instanties/exemplaren buiten de reeks.
 {  [ [=k
]x A( x) };
 (  [ [≥
k]x A( x) )
 (  [ [≤k
]x A( x) ) );
 ( k |
 (i (i :=1, ..k)
(  [ [=k]x (A(x [
i])
 (  j j ((1 ≤
j ≤ k)  (A(x [j])
 (¬( i = j)
 ¬(x [i] = x [j]
) ) ) ) j )
 (  h h (( h >
k)  (¬  A(x [h]
) ) ) h ) ) x ) i k );
 ( n, k |
 (i (i :=1, ..k)
(  [ [=k]x A(x [i
]) )
 (  j j ((1 ≤
j ≤ k)  (A(x [j])
 (¬( i = j)
 ¬(x [i] = x [j]
) ) ) ) j )
 (  h h (( k <
h ≤ n)  (¬
 A(x [h]) ) ) h ) ) x
) i k );
(Waarbij n de omvang van het referentiële domein is.
Indien dit een 'open' domein is, dan is n minstens aftelbaar oneindig, m.a.w. dan geldt ( n
≥  ) ).
Eenvoudige vorm.
'Er zijn precies ( k=) twee dingen zodat A( x)':
In een minder algemene codering:
(1) A: ' Minstens (&ge) 2 dingen zijn A':
(2) B: ' Hoogstens (&le) 2 dingen zijn A':
 x x  y y
 z z ((A( x)  A( y)
 A( z))  (( x=
y)  ( x=z)
 ( y=z)) );
(3) C: ' Precies 2 dingen zijn A:
(A  B)
 (  x x
 y y (A( x)  A( y)
 ¬( x=y))
  x x
 y y  z z ((A( x)
 A( y)  A( z))
 (( x=y)
 ( x=z)  (
y=z))) ).
Bijv.: 'Twee chalets werden beschilderd door één enkele artiest'.
(C: chalet-zij n, B: beschilderd-worden, A: artiest-zijn).
((C( d)  C( e)
  y y ((A( y)
 B( y, d)  B( y
, e))   z z (B(
z, d)  B( z, e))
 ( y=z)) ) ).
reductie:
{(  x x A( x) )  (
 [ [=k1]y A( y) ) }
 (  [ [=k1]
y A( y) ).
(·) Afleidbaarheid:
Een numeriek gekwantificeerde predicatie kan in het algemeen niet afgeleid zijn van een 'sterkere'
predicatie (met hogere generaliteit en/of zekerheid).
(·) Afgeleide(n):
Uit een numerieke predicatie is wel een zwakkere kwantificatie afleidbaar, dus met degressie:
nl. een existentiële.
Via operatie: Disjunctieve expansie.
Bijv.:
{ [k]x A(x) ) }; [k]x A(x) ) };
 ( (degres) (
 x x A( x) );
3.2.3.
Standaard kwantor eliminaties (syntactische reductie).
3.2.3.1.
Universele kwantor eliminatie (universele instantiatie).
Door een ' vrije' (universele) variabele.
Afleidbaarheid:
Universele kwantor eliminatie.
Afleiding uit Universeel gekwantificeerde variabele,
met parafrase.
Via operatie: Universele Instantiatie (UI).
via transformatie (herschrijving).
Universele kwantor eliminatie (syntactische reductie).
Universeel/ categorisch wordt Universeel/ categorisch vrije variabele.
Basisregel voor eliminatie van universele kwantor ('  elim.');
Via Universele instantiatie (UI).
Algemeen:
Bijv.: '  x x'  (UI (UI
) 'xu' is geldig.
(Mits {xu} is een vrije (nog ongebonden) variabele, ook buiten bereik van een
externe kwantor).
Bijv.: { x A(x)} x A(x)}
 ·[ x:= xu]
 (UI) (UI) A( xu) : is geldig.
(Mits {xu} is een vrije (nog ongebonden) variabele, ook buiten bereik van een
externe kwantor).
Bijv.: {  x x  y y R( x,
y) };
 ( (parafrase)(UI) R( x,
y).
(Ongeacht context: andere kwantificaties van {x,y}
mogen liggen binnen in het bereik van andere (externe) kwantoren).
Bijv.: {  x x (A( x)  B( x
))}  (UI) (UI) (A( x)
 B( y)).
Bijv.: {  x x (A( x)  B( x
))}  (UI) (UI) (A( x)
 B( x)).
Afgeleide(n):
Principe van universele generalisatie.
( Universal Generalization on a Variable, UGV).
Inverse Universele instantiatie.
Afleidbaar onder parafrase.
Bijv.: {A( x}  (UI-1) (UI-1) (
 x x A( x) ).
Universal Generalization on a variable (UGV).
(Mits {x} is een vrije (nog ongebonden) variabele, ook buiten bereik van een externe
kwantor).
3.2.3.2.
Existentiële kwantor eliminatie (Skolemisatie).
Existentiële predicaties kunnen sterk worden versimpeld in hun syntactische vorm.
Via Skolemisatie (Sk +1).
Behoort tot Kwantor-bewerkingen; met parafrase.
Hiervan zijn twee varianten.
3.2.3.2.1.
Existentiële kwantor eliminatie, via (nieuwe) 'Skolem' constante.
Indien de existentiële kwantificatie buiten het syntactische bereik ligt, dus onafhankelijk
is, van een voorafgaande ( interne of externe) universele kwantificatie,
kan haar logische kracht bij Skolemisatie in ieder geval worden behouden door middel van een (nieuwe
) ' Skolem' constante (nulplaatsige functie).
(·) Skolem constante - definitie.
Een Skolem constante, zeg c, of cs, of
cs[h], .. is een (nieuwe) 'lexicon'
constante.
Deze vertegenwoordigt in het bijzonder: een nieuwe, nog onbepaalde keuze, of selectie D [h
]·k van minstens één element d[i];
uit het volledige referentiële (sub)domein D[m]·n
.
Dus het verwijzingsgebied van cs[h], (D [h]
·k  D[m
]·n) bestaat uit één Disjunctie van àlle n elementen d
[i] uit {d [1], .. d [n] }.
Anders gezegd: Een Skolem constante verwijst naar minstens één (output
) element x, dus een onbepaalde selectie, d.i. een (ongeordende) Disjunctie van alle
(k = n) elementen van het (sub)domein.
Algemeen:
' cs' =ref (
 i i | {d [i] } i ) .
 (  h h ( c
s[h]
=ref ( n | {d [1] /d
[2] .. /d [i] .. /d [n] }
n );
=ref ( n | {
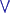 (i (i :=1, ..n)
d [i] } ) n ) ) h ).
Bijv.: {A( cs) };
 ( m, n |
 h h  k k (((( k
= n)  (  i i (d
[i]  D[m]
·n ) i )
 (D [h]·k =
{ 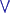 (i (i :=1, ..k)
d [i] } ) );
 A(D [h]·k );
 (( f_name(D [h]·
k ) := cs )
 A({ 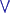 (i (i
:=1, ..k) d [i] } ) ) ) k,h
, n,m ).
[  PPL {
 i i | A [i] }.]
[  PPL {(A [1] /A
[2] ..).c0}].
[  PPL {(A1 /A2 ..).c0}].
Als er geen andere Skolem constante in de formule is:
[  PPL {(A [1] /A
[2] ..)}].
[  PPL {(A1 /A2 ..)}].
(·) Afleidbaarheid:
Afleiding uit Existentieel gekwantificeerde variabele,
die buiten het syntactische bereik ligt, dus onafhankelijk is van voorafgaande ( interne
of externe) universele kwantor(en):
Via operatie: Skolemisatie,
met een nieuwe ( Skolem) ' lexicale' constante of functie;
via transformatie ( parafrase, herschrijving).
Basisregel voor eliminatie van existentiële kwantor, '  elim.'.
Algemeen:
'  '  ' c
s' ( Skolemisatie) : is geldig.
(mits ' cs' is een (nieuwe) Skolem constante).
Bijv.: { x A(x)} x A(x)}
;
 A({d [1] /d [2] .. /d [
i] .. /d [n]} );
 ( (Sk+1) A( c
s) : is geldig.
(mits ' cs' is een (nieuwe) Skolem constante).
Kwantor-volgorde ' [ [
 ]' ]': onafhankelijkheid.
(3.2.3.2.1a) Enkelvoudige onafhankelijkheid.
Algemene regel:
S 0 = '  v [i] F[v [
i]]';
 S 0 ·[v [i] :=
c[i]];
 (Sk+1) (Sk+1) S 0·Sk =
' i |  v [n] F[
c[i]]'.
Bijv.: { x A(x)} x A(x)}
 ·[ x :=cs
]  ( (Sk+1) A( c
s) : is geldig.
(Mits { cs} is een (nieuwe) Skolem constante).
(3.2.3.2.1b) Meerdere onafhankelijken.
Algemene regel:
S 0 = '  v [1] ..
 v [n-1]  v [
n] F[v [1] .. v [n-1], v [n]]';
 S 0 ·[v [1] :=
c[1]; .. v [n-1] :=
c[n-1]];
 (Sk+1) (Sk+1) S 0·Sk =
'  v [n] F[ c[1]
, .. c[n-1], v [n]]'.
Bijv.: '  x x  y y
 z z A( x, y, z)'
 (Sk+1) (Sk+1) '  z z
A( c, d, z)'.
(3.2.3.2.1c) Meervoudige onafhankelijkheid.
Algemene regel:
S 0 = '  v [1]
 v [2] ..  v
[n] F[v [1], v [2], .. v [n]]';
 S 0 ·[v [1] :=
c[1] ];
S 0 =  (Sk+1) (Sk+1) '
 v [2] .. 
v [n] F[ c[1], v [2], .. v [n]
]';
Bijv.: '  x x  y y
 z z A( x, y, z)'
 (Sk+1) (Sk+1) '  y y
 z z A( c, y, z)'.
(·) Afgeleide(n):
Uit een Skolem constante is geen 'zwakkere' expressie afleidbaar.
3.2.3.2.2.
Existentiële kwantor eliminatie, via (nieuwe) (meerplaatsige) 'Skolem' functie
.
Indien de existentiële kwantificatie ligt binnen het syntactische bereik, dus afhankelijk is,
van een voorafgaande ( interne of externe) universele kwantificatie, kan haar logische kracht
bij Skolemisatie hoogstens worden behouden door middel van een (nieuwe) meerplaatsige
Skolem functie.
(·) Skolem functie - definitie.
Een Skolem functie, zeg f( x), of fs
( x), of fs[h]( x), ..
is een (nieuwe) ' lexicon' functie.
Deze vertegenwoordigt altijd per argument binnen de argumentlijst van de functieterm, voor elk
element d[i] uit het betreffende (sub)domein D[m]
·n: steeds weer precies één nieuwe, nog onbepaalde keuze, of
selectie; D [h,i]·k, van minstens één element d
[j[i]]; uit het volledige betreffende (sub)domein D[m]
·n.
Dus het verwijzingsgebied van fs[h]( x
), (D [h]·n  D
[m]·n) bestaat uit één Conjunctie van àlle
n afzonderlijke elementen D [h,i]·k,
die alle bestaan uit een Disjunctie, van (maximaal) àlle k= n elementen d [j
] uit {d [1], .. d [k] }.
Anders gezegd: Een Skolem functie verwijst via elk (input) element x
steeds opnieuw naar minstens één (output) element y, dus een onbepaalde
selectie, d.i. een (ongeordende) Disjunctie van alle (k = n
) elementen van het (sub)domein.
(Met andere woorden, elke éénplaatsige Skolem functie fs
( x) op een domein D ·n is te beschouwen als een Conjunctie met voor
elke x [i] uit n een afzonderlijke Skolem constante c
s[i].
Deze zijn niet onderling te unificeren).
Algemeen:
' fs( x)'
=ref ( n | f
s({ x [1] ,x [2] .. ,x [n]
} ) n );
=ref ( n | { f
s(x [1]), fs(x [2]
), .. fs(x [n]) }
n );
=ref ( n | {
 (i (i :=1, ..n)
| fs[h](x [i])
i } n ).
=ref ( n, k, (
 i i ( k[i] = n )
i ) |
{{d[1[1]] /d[2[1]] .. /d[k[1]]} ,{d[1[2]] /
d[2[2]] .. /d[k[2]]} .. ,{d[1[n]]
/d[2[n]] .. /d[k[n]]} }k,n
);
 {  h h (f s
[h]( x)
=ref ( n | f
s[h]({ x [1] ,x [2] .. ,x [
n] } ) n );
=ref ( n | { f
s[h](x [1]) , fs[
h](x [2]) .. , fs[h]
(x [n]) } n );
=ref ( n | {
 (i (i :=1, ..n)
| fs[h](x [i]
) i } n );
=ref ( n, k, (
 i i ( k[i] = n )
i ) |
{{d[1[1]] /d[2[1]] .. /d[k[1]]} ,{d[1[2]]
/d[2[2]] .. /d[k[2]]} .. ,{d[1[n]]
/d[2[n]] .. /d[k[n]]} }k,
n );
=ref ( n, k, (
 i i ( k[i] = n )
i ) |
{{ 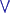 (j[1]:=1, (j[1]:=1, ..k[1]) d [j[1]]
} ,{ 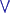 (j[2]:=1, (j[2]:=1, ..k[2]) d [j
[2]]} .. ,{ 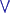 (j[n]:=1, (j[n]:=1,
..k[n]) d [j[n]]} } k,n );
=ref ( n, k, (
 i i ( k[i] = n )
i ) |  (i (i
:=1, ..n) 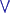 (j[i
]:=1, (j[i
]:=1, ..k[n]) {d [j[i]] } k,n ).
=ref ( n, k | {
 (i (i :=1, ..n)
(( k[i] = n ) | (
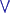 (j[i]:=1, (j[i]:=1, ..k[i]) {d
[j[i]]} ) ) i } k, n );
=ref ( n, ( k=n)
| {D [h,1]·k ,D [h,2]
·k .. ,D [h,n]·k
} n );
=ref ( n | { c
s[h,1] , cs
[h,2] .. , cs[h
,n] } n );
=ref ( n | (
 (i (i :=1, ..n)
cs[h,i] ) i
) n ) h }.
Bijv.: {A( fs( x)) };
 ( n | A( fs
({ x [1] ,x [2] .. ,x [n] } ) )
n );
 ( n | A({ fs
(x [1]) , fs(x [2])
.. , fs(x [n]) } n
);
 ( n | {A( fs
(x [1])) ,A( fs(x [2]))
.. ,A( fs(x [n])) }
n );
 ( n |
 (i (i :=1, ..n)
A( fs(x [i])) i,
n );
 ( m, n |
 h h (  k k (
 i i (( k[i] = n )
 (d [i]  D
[m]·n )
 (D [h,i]·k[i]
= { 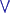 (j (j :=1, ..
k[i] ) d [j] } ) );
 (( fs(x [
i] ) :=D [h,i]·k[i]
)  A(D [h,i]·k[
i] ) ) ) i ) k );
 ( k, ( k = n ) |
{  (i (i :=1, ..
n) A(D [h,i]·k ) i }
k );
 {  (i (i
:=1, ..n) A( cs
[h,i] ) i } ) h, n,m
).
[  PPL {( x=1:(A [1]
/A [2] ..).f) ,( x=2:(A [1] /A [2] ..).f) ..
}];
[  PPL {(A [1] /A
[2] ..).1f ,(A [1] /A [2] ..).2f .. }];
[  PPL {(A1/A2/ ..).1f)
,(A1/A2/ ..).2f) .. }];
Als er geen andere Skolem functie in de formule is:
[  PPL {(A [1] /A
[2] ..).1 ,(A [1] /A [2] ..).2 .. }];
[  PPL {(A1/A2/ ..).1
,(A1/A2/ ..).2 .. }];
(·) Afleidbaarheid:
Afleiding uit Existentieel gekwantificeerde variabele,
die binnen het syntactische bereik ligt, dus afhankelijk is van voorafgaande ( interne
of externe) universele kwantor(en):
met parafrase.
Via operatie: Skolemisatie;
via transformatie (herschrijving).
Algemeen:
'   '
 ' fs()' ( Skolemisatie)
: is geldig.
(mits ' fs()' is een (nieuwe) Skolem constante).
Kwantor-volgorde '
 ' ': afhankelijkheid.
(3.2.3.2.2a) Enkelvoudige afhankelijkheid.
Algemene regel:
S 0 = '  v [1]
 v [2] F[v [1], v [2]]';
 S 0 ·[v [2] :=
fs(v [1]) ];
 (Sk+1) (Sk+1) S 0·Sk =
'  v [1] F[ fs(v [1]
) ]'.
Bijv.: {  x x  y y A( y
) };
 ·[ y :=fs
( x)];  (Sk+1) (Sk+1) A( f
s( x)));
(Mits { fs()} is een (nieuwe) Skolem functie).
(3.2.3.2.2b) Meervoudige afhankelijkheid.
Een Existentieel gekwantificeerde variabele die van meerdere Universele kwantoren afhankelijk is,
vereist introductie van een evenredig veelplaatsige nieuwe Skolem functie.
Algemene regel:
S 0 = '  v [1] ..
 v [n-1]  v [
n] F[v [1] .. v [n-1], v [n]]';
 S 0 ·[v [n] :=
fs(v [1], .. v [n-1]
) ];
 (Sk+1) (Sk+1) S 0·Sk =
'  v [1] ..
 v [n-1] F[ fs
(v [1], .. v [n-1]) ]'.
Bijv.: S 0 = '  x x
 y y  z z A( x, y
, z)';  (Sk+1) (Sk+1) S 0·Sk
= '  x x  y
y A( x, y, fs( x, y))'.
Bijv.: '  x x  y y
 z z  w w A( w, y
, z, x)';  (Sk+1) (Sk+1) '
 x x  y y
 w w A( w, y, fs1
( x,y), x)'.
(3.2.3.2.2c) Meerdere afhankelijken.
Een aantal Existentieel gekwantificeerde variabelen die van dezelfde Universele kwantor afhankelijk is,
vereist introductie van een evenredig veel nieuwe Skolem functies.
Algemene regel:
S 0 = '  v [1]
 v [2] ..  v
[n] F[v [1], v [2], .. v [n]]';
 S 0 ·[v [2] :=
fs[1](v [1]); .. v [n]
:= fs[ n-1](v [1])];
 (Sk+1) (Sk+1) S 0·Sk =
'  v [1] F[ fs
[1](v [1]), .. fs[ n
-1](v [1]) ]'.
Bijv.: '  x x  y y
 z z A( x, y, z)';
 (Sk+1) (Sk+1) '  x x
A( x, fs( x), gs
( y))'.
Bijv.: '  x x  y y
 z z  w w A( w, y
, z, x)';  (Sk+1) (Sk+1) '
 x x  z z A( f
s2( x,z), fs1( x), z
, x)'.
Bijv.: '  x x  y y
 z z  w w A( z, x
, w, y)';  (Sk+1) (Sk+1) '
 x x  y y A( f
s1( x,y), x, fs2( x
,y), y)'.
(·) Afgeleide(n):
Uit een Skolem functie met n argumenten {v [1], v [2], ..
v [n] } is een evenredig aantal Existentieel gekwantificeerde variabelen, c.q.
(nieuwe) Skolem constanten afleidbaar - op grond van subsumptie.
Afleidbaar onder parafrase.
[*nog regel +vb.n pasten uit elders.]
3.2.4.
Constanten en Functies in de logica.
3.2.4.1. 'Normale'
logische constante.
Een 'constante' is in feite een nulplaatsige functie.
(·) (Domein) constante - definitie.
Een 'normale' constante, of nul-plaatsige logische functie, zeg c, of c
d, of cd[h], .. is een (bestaande) ' domein
' constante.
Deze vertegenwoordigt in het bijzonder: precies één specifieke, definiete keuze, of selectie C
[i]·k; d.i. een niet-lege (ongeordende) subset,
sample c.q. Conjunctie van minstens één element d[i];
uit het volledige betreffende (sub)domein D[m]·n
.
Dus het verwijzingsgebied van cd[h], (C [h]
·k  D[m]
·n) bestaat uit één Conjunctie van sommige van de n
elementen d [i] uit {d [1], .. d [n] }.
(In principe kan een 'domein' constante ook verwijzen naar een lege verzameling c.q. (sub)domein,
maar het betreft in dat geval een afwijkende vorm, c.q. anomalie: dit type maakt de betreffende predicatie
altijd onwaar, waardoor ze niet in alle formules substitueerbaar is).
Anders gezegd: Een 'domein' constante verwijst naar minstens één (output) element
x, dus een bepaalde selectie, d.i. een (ongeordende) Conjunctie van sommige
(1 ≤ k ≤ n) elementen van het (sub)domein.
Algemeen:
' cd' =ref (i |
{d[i], .. }i ) .
 {  h h ( c
d[h]
=ref ( n, k | ((1
≤ k ≤ n) | C [h]
·k ) k,n );
=ref ( n, k | ((1
≤ k ≤ n) | {
 (i (i :=1, ..k)
d [i] } ) k,n ) ) h }.
Bijv.: {A( cd) };
 ( m, n, |
 h h  k k ((((1 ≤
k ≤ n)  (C [h]
·k  D[m
]·n )
 (C [h]·k = {
 (i (i :=1, ..k)
d [i] } ) );
 A(C [h]·k ) );
 (( f_name(C [h]·k
) := cd )
 A({  (i (i :=
1, ..k) d [i] } ) ) ) k,h,
n,m );
[ PPL
{ i | A[i]};]
(·) Afleidbaarheid:
Een 'domein' constante wordt per definitie ingevoerd en kan dus niet worden afgeleid.
Een predicatie met een 'domein' constante kan wel worden afgeleid, met degressie, uit een (meer algemene)
predicatie, via substitutie, m.n. instantiatie.
Via operatie: Conjunctieve reductie.
(·) Afgeleide(n):
Afleiding uit 'domein' constante, met degressie.
Via operatie: Disjunctieve expansie.
3.2.4.2. '
Normale' logische functie.
Een 'functie' is in de gebruikelijke betekenis meerplaatsig.
(·) (Domein) functie - definitie.
Een 'normale' één-plaatsige functie, zeg f( x), of fd
( x), of fd[h]( x), ..
is een (bestaande) ' domein' functie.
Deze vertegenwoordigt altijd per argument x binnen de argumentlijst van de functieterm,
voor elk element d[i] uit het betreffende (sub)domein D[
m]·n: steeds weer precies één specifieke, definiete keuze, of
selectie; C [h,i]·k[i], van minstens één
element d [j[i]]; uit het volledige betreffende (sub)domein D[m
]·n.
Dus het verwijzingsgebied van fd[h]( x), (C [h
]·k  D[
m]·n) bestaat uit één Conjunctie van àlle n elementen C
[h,i]·k met per element (C [h,i]
·k  C [h]·k
) een Conjunctie, van (minimaal) tenminste één element d [j] uit {
d [1], .. d [k] }.
Anders gezegd: Een 'domein' functie verwijst via elk (input) element x steeds opnieuw
naar minstens één (output) element y, dus een bepaalde selectie,
d.i. een (ongeordende) Conjunctie van sommige (1 ≤ k ≤ n) elementen
van het (sub)domein.
(In principe kan een 'domein' functie ook, voor een bepaalde parameterset (bijv. x),
verwijzen naar een lege verzameling c.q. (sub)domein, maar het betreft in dat geval
een afwijkende vorm, c.q. anomalie: dit type maakt de betreffende predicatie altijd onwaar,
waardoor ze niet in alle formules substitueerbaar is).
Algemeen:
' fd( x)'
=ref ( n | f
d({ x [1] ,x [2] .. ,x [n] } ) n
);
=ref ( n | { f
d(x [1]), fd(x [2]), ..
fd(x [n]) } n );
=ref ( n | {
 (i (i :=1, ..n)
| fd(x [i]) i }
n ).
=ref ( n, k, (
 i i (1 ≤ k[i]
≤ n ) i ) |
{{d[1[1]] ,d[2[1]] .. ,d[k[1]]} ,{d[1[2]] ,d
[2[2]] .. ,d[k[2]]} .. ,{d[1[n]]
,d[2[n]] .. /d[k[n]]} }k,n
);
 {  h h | (
fd[h]( x)
=ref ( n | f
d[h]({ x [1] ,x [2] .. ,x [n] } )
n );
=ref ( n | { f
d[h](x [1]) , fd[h](x [2])
.. , fd[h](x [n]) } n );
=ref ( n | {
 (i (i :=1, ..n)
| fd[h](x [i]) i
} n );
=ref ( n, k, (
 i i (1 ≤ k[i]
≤ n ) i ) |
{{d[1[1]] ,d[2[1]] .. ,d[k[1]]} ,{d[1[2]] ,
d[2[2]] .. ,d[k[2]]} .. ,{d[1[n]]
,d[2[n]] .. /d[k[n]]} }k,n
);
=ref ( n, k, (
 i i (1 ≤ k[i]
≤ n ) i ) |
{{  (j[1]:=1, (j[1]:=1, ..k[1]) d [j[1]]}
,{  (j[2]:=1, (j[2]:=1, ..k[2]) d [j[2]]}
.. ,{  (j[n]:=1, (j[n]:=1, ..k[
n]) d [j[n]]} } k,n );
=ref ( n, k, (
 i i (1 ≤ k[i]
≤ n ) i ) |  (i
(i :=1, ..n)
 (j[i]:=1, (j[i]:=1, ..k[n]) {d
[j[i]] } k,n ).
=ref ( n | {
 (i (i :=1, ..n)
(  k k ((1 ≤ k[i]
≤ n) | (  (j[
i]:=1, (j[
i]:=1, ..k[i]) {d [j[i]] } ) ) k
) i } n );
=ref ( n, ( k=n)
| {C [h,1]·k ,C [h,2]
·k .. ,C [h,n]·k }
n );
=ref ( n | { c
d[h,1] , cd[h,2] ..
, cd[h,n] } n );
=ref ( n | (
 (i (i :=1, ..n)
cd[h,i] ) i ) n
) h }.
Bijv.: {A( fd( x))};
 ( n | A( fd[h]
({ x [1] ,x [2] .. ,x [n] } ) ) n
);
 ( n | A({ fd(x
[1]) , fd(x [2]) .. , f
d(x [n]) } n );
 ( n | {A( fd(x
[1])) ,A( fd(x [2])) .. ,A( f
d(x [n])) } n );
 (  (i (i :=
1, ..n) A( fd(x [i]))
i );
 ( m, n |
 h h ((  i i
 k k ((((1 ≤ k[i]
≤ n)  (C [h,i]
·k[i]  D[m
]·n )
 (C [h,i]·k[i]
= {  (j (j :=1, ..
k[i] ) d [j] } ) );
 (( fd(x [i] )
:=C [h,i]·k[i] )
 A(C [h,i]·k[i]
) ) ) k,i );
 (  (i (i
:=1, ..n) (  k k ((1
≤ k[i] ≤ n)
 A(C [h,i]·k[i]
) k ) i );
 {  (i (i
:=1, ..n) A( cd[h,i
] ) i } ) h, n,m ).
[ PPL
{(x=1:(A[1[1]] ,A[2[1]] ..)) ,(x=2:(A[1[2]] ,A
[2[2]] ..)) .. }];
(·) Afleidbaarheid:
Een 'domein' functie wordt per definitie ingevoerd en kan dus niet worden afgeleid.
Een predicatie met een 'domein' functie kan wel worden afgeleid, met degressie, uit een (meer algemene)
predicatie. Via domeininterpretatie, via substitutie, m.n. instantiatie
- of indien nodig andere technieken zoals subsumptie.
Via operatie: Conjunctieve reductie.
Impliceert degressie.
Algemeen:
' x'  ( (degres) ' f
d( x))' ( instantiatie): is geldig.
' xu'  ( (degres) '
fd( x))' ( instantiatie): is geldig.
(' fd( x))' kan een (bestaande) domein functie zijn).
Bijv.: {A(xu)}
·[ xu:= fd( x))]
 ( (degres) A( fd(
x))).
(·) Afgeleide(n):
Afleiding uit 'domein' functie, met degressie.
Via operatie: disjuncte expansie.
 {  h h | (
fd[h]( x)
 ( (degres)
( x x  y (x,
yx) )y,x )h }. y (x,
yx) )y,x )h }.
Bijv.: {A( fd( x))}; [
 PPL {(x=1:(A[j[1
]])), (x=2:(A[j[2]])), .. }];
3.2.5.
Codering van modale operatoren.
We kunnen voor modale uitdrukkingen een apart symbool, zeg ' Cm
' gebruiken om een algemene, onbepaalde ('anonieme') voorwaarde weer te geven.
3.2.5.1.
Modale operator van Noodzakelijkheid.
'Het is noodzakelijk dat A':
D.w.z. 'Onder èlke conditie is A het geval'.
 '  x x ( C
m( x)  A A)';
 '  x x (¬ C
m( x)  A A)';
 '¬  x x ¬(¬ C
m( x)  A A)';
 '¬  x x ( C
m( x)  ¬ A)'.
Bijv.:  ( x |
 y y ( Cm( x,
y))  A( x)) ).
3.2.5.2.
Modale operator van Mogelijkheid.
'Het is mogelijk dat A':
D.w.z. 'Er is minstens één conditie waaronder A het geval is'.
 '  x x ( C
m( x)  A A)';
 '  x x (¬ C
m( x)  A A)';
 '¬  x x ¬(¬ C
m( x)  A A)';
 '¬  x x ( C
m( x)  ¬ A)'.
Niet een adequate vertaling is:
'((  x x ¬ Cm(
x))  A A)';
 '((¬  x x ¬¬ C
m( x))  A A)';
 '((¬  x x C
m( x))  A A)';
 '((¬(  x x C
m( x)))  A A)';
 '(¬(  x x C
m( x))  A A)';
 '((  x x C
m( x))  A A)';
 '(  x x ( C
m( x)  A A))';
Bijv.:  ( x |
 y y ( Cm( x,
y))  A( x)) ).
C.P. van der Velde © 2004, 2016, 2019.
|
|